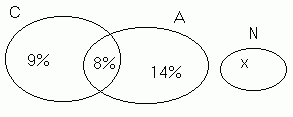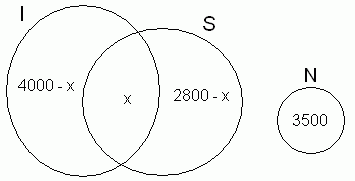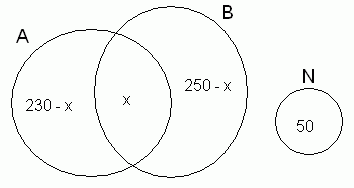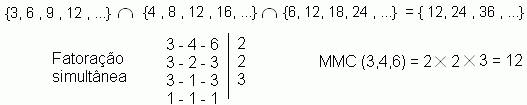EXERCÍCIOS SOBRE A TEORIA DE CONJUNTOS E ARITMÉTICA BÁSICA
Fonte: Prof. Ezequias
(FATEC) Para a identificação de pacientes com sintomas de gripe influenza A, a Anvisa (Agência Nacional de Vigilância Sanitária) informou hoje que os voos procedentes do Reino Unido, Espanha e Nova Zelândia também serão inspecionados por uma equipe da agência e por médicos da Empresa Brasileira de Infraestrutura Aeroportuária (Infraero).
Inicialmente, apenas os voos vindos do México, Canadá e Estados Unidos eram inspecionados. A decisão foi tomada durante reunião da Anvisa com representantes das companhias aéreas, da Agência Nacional de Aviação Civil (Anac) e da Infraero, no Aeroporto Internacional de Cumbica, em Guarulhos, na Grande São Paulo.
(Adaptado de: http://noticias.uol.com.br/cotidiano/2009/04/28/ult5772u3774.jhtm, Acesso em: 09.05.2009.)

diagrama de Venn-Euler Em um voo proveniente de Miami, a Anvisa constatou que entre todas as pessoas a bordo (passageiros e tripulantes) algumas haviam passado pela cidade do México.
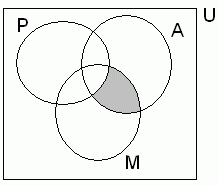
No diagrama, U representa o conjunto das pessoas que estavam nesse voo; P o conjunto dos passageiros; M o conjunto das pessoas que haviam passado pela cidade do México e A o conjunto das pessoas com sintomas da gripe influenza A. Considerando verdadeiro esse diagrama, conclui-se que a região sombreada representa o conjunto das pessoas que, de modo inequívoco, são aquelas caracterizadas como
(A) passageiros com sintomas da gripe que não passaram pela cidade do México.
(B) passageiros com sintomas da gripe que passaram pela cidade do México.
(C) tripulantes com sintomas da gripe que passaram pela cidade do México.
(D) tripulantes com sintomas da gripe que não passaram pela cidade do México.
(E) tripulantes sem sintomas da gripe que passaram pela cidade do México.

Solução: No diagrama, a região sombreada está fora do conjunto P, logo, não representa passageiros, e sim tripulantes. Como essas pessoas estão dentro do conjunto A e do conjunto M (dentro do conjunto interseção AÇM), então, a região sombreada representa tripulantes com sintomas da gripe que passaram pela cidade do México (alternativa C).
(PUC) Um levantamento sócio-econômico entre os habitantes de uma cidade revelou que, exatamente: 17% têm casa própria; 22% têm automóvel; 8% têm casa própria e automóvel. Qual o percentual dos que não têm casa própria nem automóvel?
Solução: Com base nos dados, fazemos um diagrama de Venn-Euler, colocando a quantidade de elementos dos conjuntos, começando sempre pelo número de elementos da interseção n(CÇA) = 8%.

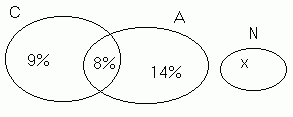
Diagrama de Venn - Euler. Começamos sempre colocando o número de elementos da intersecção. Ao colocar o número de elementos de um conjunto, não podemos esquecer de descontar os da intersecção.

Como a soma das parcelas percentuais resulta em 100%, então 9% + 8% + 14% + x = 100 %. Daí, vem que 31% + x = 100%. Logo, o percentual dos que não têm casa própria nem automóvel é x = 100% - 31% = 69%.

Uma editora estuda a possibilidade de lançar novamente as publicações Helena, Senhora e A Moreninha. Para isto, efetuou uma pesquisa de mercado e concluiu que em cada 1000 pessoas consultadas: 600 leram A Moreninha; 400 leram Helena; 300 leram Senhora; 200 leram A Moreninha e Helena; 150 leram A Moreninha e Senhora; 100 leram Senhora e Helena; 20 leram as três obras; Calcule:
a) O número de pessoas que leu apenas uma das obras.
b) O número de pessoas que não leu nenhuma das três obras.
c) O número de pessoas que leu duas ou mais obras.
Solução: Começamos sempre colocando o número de elementos da intersecção. Ao colocar o número de elementos de um conjunto, não podemos esquecer de descontar os da intersecção
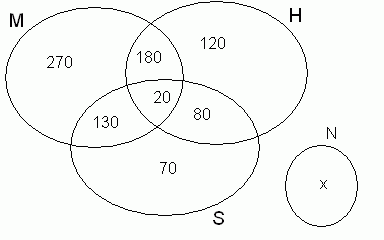Diagrama onde: M = Moreninha, H = Helena e S = Senhora. 200 - 20 = 180 ;
150 - 20 = 130 ;
100 - 20 = 80 ;
600 - 180 - 20 - 130 = 270 ;
400 - 180 - 20 - 80 = 120 ;
300 - 130 - 20 - 80 = 70.
270 + 180 + 120 + 130 + 20 + 80 + 70 = 870
Assim:
a) O número de pessoas que leu apenas uma das obras é 270 + 120 + 70 = 460 :
b) O número de pessoas que não leu nenhuma das três obras é x = 1000 - 870 = 130 ;
c) O número de pessoas que leu duas ou mais obras é 180 + 20 + 130 + 80 = 410

Dez mil aparelhos de TV foram examinados depois de um ano de uso e constatou-se que 4.000 deles apresentavam problemas de imagem, 2.800 tinham problemas de som e 3.500 não apresentavam nenhum dos tipos de problema citados. Então o número de aparelhos que apresentavam somente problemas de imagem é:
a) 4 000                b) 3 700                c) 3 500                d) 2 800            e) 2 500
Solução:  Resposta na altermativa b). Observe o diagrama construído com base no enunciado, onde I é o conjunto dos que apresentavam defeito na imagem, S o conjunto dos que apresentavam problemas de som e N o conjunto daqueles que não apresentavam nenhum defeito citado.

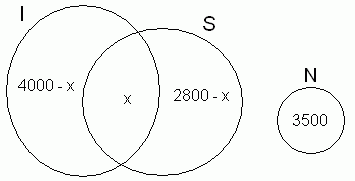
Temos que  4000 - x + x + 2800 - x + 3500 = 10000, onde x é o números de televisores que apresentavam, ao mesmo tempo, os dois problemas citados. Segue que x = 10300 - 10000 = 300. Então o número de aparelhos que apresentavam somente problemas de imagem é 4000 - x = 4000 - 300 = 3700.  

Numa pesquisa sobre as emissoras de tevê a que habitualmente assistem, foram consultadas 450 pessoas, com o seguinte resultado: 230 preferem o canal A; 250 o canal B; e 50 preferem outros canais diferente de A e B. Pergunta-se:
a) Quantas pessoas assistem aos canais A e B?
b) Quantas pessoas assistem ao canal A e não assistem ao canal B?
c) Quantas pessoas assistem ao canal B e não assistem ao canal A?
d) Quantas pessoas não assitem ao canal A?

Solução: Seja o diagrama a seguir: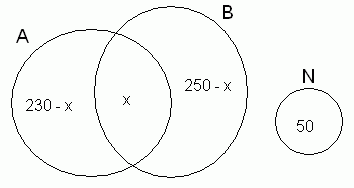

Temos que 230 - x + x + 250 - x + 50 = 450.
a) O número de pessoas que assistem aos canais A e B é x = 530 - 450 = 80
b) O número de pessoas que assistem ao canal A e não assistem ao canal B é 230 - x = 150.
c) O número de pessoas que assistem ao canal B e não assistem ao canal A é 250 - x = 170.
d) O número de pessoas que não assitem ao canal A é 250 - x + 50 = 250 - 80 + 50 = 220.

(PUC) Numa comunidade constituída de 1800 pessoas há três programas de TV favoritos: Esporte (E), novela (N) e Humanismo (H). A tabela abaixo indica quantas pessoas assistem a esses programas.
Programas  E   N  H E e N E e H N e H E, N e H Nenhum
Número de telespectadores 400 1220 1080   220  180  800      100   x

Através desses dados verifica-se que o número de pessoas da comunidade que não assistem a qualquer dos três programas é:
(A) 200   (C) 900  
(B) os dados do problema estão incorretos. (D) 100                   (E) n.d.a.

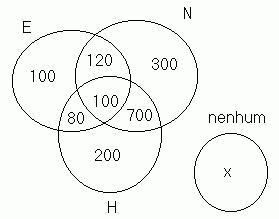
Solução: No diagrama de Venn-Euler colocamos a quantidade de elementos dos conjuntos, começando sempre pela interseção que tem 100 elementos.

Diagrama de Venn - Euler. Começamos sempre colocando o número de elementos da intersecção. Ao colocar o número de elementos de um conjunto, não podemos esquecer de descontar os da intersecção Então, 100 + 120 + 100 + 80 +700 + 200 + 300 + x = 1800. Segue que, 1600 + x = 1800. Logo, o número de pessoas da comunidade que não assistem a qualquer dos três programas é: x = 1800 - 1600 = 200.
Assim, (A) é a opção correta.

(PUC) Em uma empresa, 60% dos funcionários lêem a revista A, 80% lêem a revista B, e todo funcionário é leitor de pelo menos uma dessas revistas. O percentual de funcionários que lêem as duas revistas é ....
Solução: Seja x o valor procurado. Desenhando um diagrama de Venn-Euler e utilizando-se do fato de que a soma das parcelas percentuais resulta em 100%, temos a equação: 60 - x + x + 80 - x = 100. Daí, vem que, 60 + 80 - x = 100.

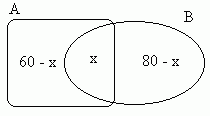
diagrama de Venn-Euler.

Logo, x = 140 - 100 = 40. Assim, o percentual procurado é 40%.

(UFMG) Numa república hipotética, o presidente deve permanecer 4 anos em seu cargo; os senadores, 6 anos e os deputados, 3 anos. Nessa república, houve eleição para os três cargos em 1989.
A próxima eleição simultânea para esses três cargos ocorrerá, novamente, em que ano?
Solução: Temos que encontrar um número que é múltiplo de 3, de 4 e de 6 ao mesmo tempo, e mais, este número deverá ser o menor deles, ou seja, temos que encontrar o mínimo múltiplo comum de 3, 4 e 6.
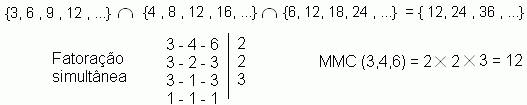
2x2x3=12
Fatorando 3 , 4 e 6 simultaneamente encontramos 22× 3. Logo, M.M.C. (3 , 4 , 6) = 12. Assim, a próxima eleição simultânea acontecerá em 1989 + 12 = 2001.
Em uma prova de Matemática com apenas duas questões, 300 alunos acertaram somente uma das questões e 260 acertaram a segunda. Sendo que 100 alunos acertaram as duas e 210 alunos erraram a primeira questão. Quantos alunos fizeram a prova?
Solução: Temos que 100 acertaram as duas questões. Se 260 acertaram a segunda, então, 260 - 100 = 160 acertaram apenas a segunda questão. Se 300 acertaram somente uma das questões e 160 acertaram apenas a segunda, segue que, 300 - 160 = 140 acertaram somente a primeira. Como 210 erraram a primeira, incluindo os 160 que também erraram a primeira, temos que, 210 - 160 = 50 erraram as duas. Assim podemos montar o diagrama de Venn-Euler, onde: P1 é o conjunto dos que acertaram a primeira questão; P2 é o conjunto dos que acertaram a segunda e N é o conjunto dos que erraram as duas. Observe a interseção P1Ç P2 é o conjunto dos que acertaram as duas questões.

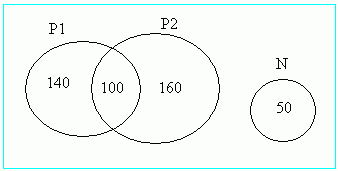
diagramas de conjuntos

Logo, o número de alunos que fizeram a prova é: 140 + 100 + 160 + 50 = 450.

Inscreveram-se num concurso público 700 candidatos para 3 cargos - um de nível superior, um de nível médio e um de nível fundamental. É permitido aos candidatos efetuarem uma inscrição para nível superior e uma para nível médio. Os candidatos ao nível fundamental somente podem efetuar uma inscrição. Sabe-se que 13% dos candidatos de nível superior efetuaram 2 inscrições. Dos candidatos de nivel médio, 111 candidatos efetuaram uma só inscrição, correspondendo a 74% dos candidatos desse nível. Qual é então o número de candidatos ao nível fundamental?
Solução: Sejam: #(M) o número de candidatos de nível médio; #(SÇM) o número de candidatos aos níveis superior e médio; #(S) o número de candidatos ao nível superior; #(F) número de candidatos ao nível fundamental. Da Matemática Financeira sabemos que: 74% = 74/100 = 0,74 e 13% = 13/100 = 0,13.
Então, 0,74×#(M) = 111, segue que, #(M) = 111 / 0,74 = 150 e #(SÇM) = 150 - 111 = 39 .
Assim, 0,13×#(S) = 39, implicando em #(S) = 39 / 0,13 = 300 . Observe o diagrama de Venn-Euler com a quantidade de elementos.

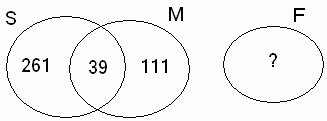
Temos: 300 - 39 = 261. Logo, 261 + 39 + 111 + #(F) = 700. Consequentemente, #(F) = 700 - 411 = 289.
No último clássico Corinthians × Flamengo, realizado em São Paulo, verificou-se que só foram ao estádio paulistas e cariocas e que todos eles eram só corintianos ou só flamenguistas. Verificou-se também que, dos 100.000 torcedores, 85.000 eram corintianos, 84.000 eram paulistas e que apenas 4.000 paulistas torciam para o Flamengo. Pergunta-se:

a) Quantos paulistas corintianos foram ao estádio?

b) Quantos cariocas foram ao estádio?

c) Quantos não-flamenguistas foram ao estádio?

d) Quantos flamenguistas foram ao estádio?

e) Dos paulistas que foram ao estádio, quantos não eram flamenguistas?

f) Dos cariocas que foram ao estádio, quantos eram corintianos?

g) Quantos eram flamenguistas ou cariocas?

h) Quantos eram corintianos ou paulistas?

i) Quantos torcedores eram não-paulistas ou não-flamenguistas?

Solução: Devemos construir uma tabela com os dados do enunciado e as diferenças:

Cariocas Paulistas Totais
Flamenguistas 11.000 4.000 15.000
Corintianos 5.000 80.000 85.000
Totais 16.000 84.000 100.000

Com base na tabela, podemos responder todas as perguntas, levando em conta que:

I) O conectivo "e" está sempre associado a interseção de conjuntos e o conectivo "ou" está  sempre associado a união de conjuntos.

II) n(A È B) = n(A) + n(B) - n(A Ç B).

a) "Cruzando os dados" na tabela, vemos que o número de paulistas e corintianos é 80.000.

b) O total de cariocas é 16.000 .

c)  O total de não-flamenguistas, ou seja , corintianos é 85.000.

d) O total de flamenguistas é 15.000.

e) O número de paulistas e não flamenguista, isto é, paulistas e corintianos é 80.000.

f) O número de cariocas e corintianos é 5.000.

g)  O número de flamenguistas ou cariocas é 15.000 + 16.000 - 11.000 = 20.000.

h)  O número de paulistas ou corintianos 84.000 + 85.000 - 80.000 = 89.000 .

i) O número de cariocas ou corintianos é 16.000 + 85.000 - 5.000 = 96.000.

(UFRJ - adaptado) Um clube oferece a seus associados aulas de três modalidades de esporte: natação, tênis e futebol. Nenhum associado pôde se inscrever simultaneamente em tênis e futebol, pois, por problemas administrativos, as aulas destes dois esportes serão dadas no mesmo horário. Encerradas as inscrições, verificou-se que: dos 85 inscritos em natação, 50 só farão natação; o total de inscritos para as aulas de tênis foi de 17 e, para futebol, de 38; o número de inscritos só para as aulas de futebol excede em 10 o número de inscritos só para as de tênis.

a) Quantos associados se inscreveram  simultaneamente para aulas de futebol e natação?

b) Quantos associados se inscreveram  simultaneamente para aulas de tênis e natação?

Solução: Com base nos dados, fazemos um diagrama de Venn-Euler, colocando a quantidade de elementos dos conjuntos, começando sempre pelo número de elementos da interseção. Como nenhum associado pôde se inscrever simultaneamente em tênis e  futebol, então n(TÇF) = 0  e  n(TÇNÇF) = 0.

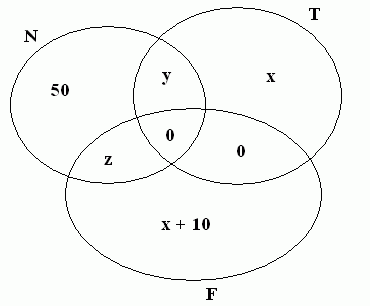
Observando o diagrama, temos o sistema de equações:

z + y + 50 = 85

z + y = 35

x + y = 17

z  + x +10 = 38

z + x = 28

Somamdo a segunda equação com a terceira obtemos

z + x  + y + y = 35 + 17

z + x + 2y = 52

Como z + x = 28, então:

28 + 2y = 52

2y = 52 - 28

2y = 24

y = 12

Substituindo na terceira equação, segue que:

x + 12 = 17

x = 17 - 12 = 5

Substituindo na quinta equação, ficamos com:

z + 5 = 28

z = 28 - 5 = 23.

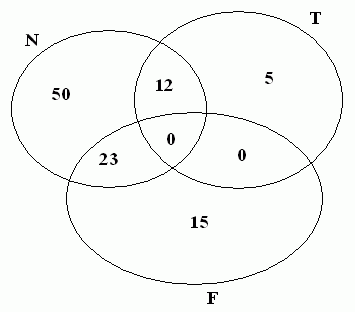
Assim, a) 23 associados se inscreveram  simultaneamente para aulas de futebol e natação;

b) 12 associados se inscreveram  simultaneamente para aulas de tênis e natação.

Uma montadora de automóveis lançou no mercado um novo veículo em três versões: a versão simples MS; a luxuosa ML e a super luxuosa SL. Cada versão pode ser adquirida em uma dentre três cores: azul, vermelha ou preta. Consideremos que um consumidor escolha em primeiro lugar uma das versões (MS, ML OU SL). E em segundo lugar umas das cores (azul, vermelha ou preta). Quais as possibilidades de escolha?
Solução : Considerando A o conjunto das versões de automóveis e B o conjunto de suas cores,  o resultado procurado está no produto cartesiano A×B, ou seja, no conjunto dos pares ordenados (x , y), onde o primeiro elemento de cada par pertence a A e o seguinte a B.

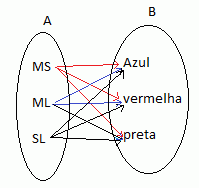
produto cartesiano

Então, as possibilidades de escolha estão no conjunto:

A×B = {(MS, azul), (MS, vermelha), (MS, preta), (ML, azul), (ML, vermelha), (ML, preta), (SL, azul), (SL, vermelha), (SL, preta)}.