Sequências

            A ocorrência de acontecimentos que se repetem periodicamente em nosso cotidiano possui estreita relação com a matemática, no que se refere à sucessão de percepções diversas, tais como o passar do tempo, a rotina diária de trabalho e até mesmo os fatos menos perceptíveis como a nossa respiração, o batimento de nosso coração e assim sucessivamente.

            Assim, a sequência (ocorrência periódica) de fatos em nosso cotidiano nos conduz, principalmente à idéia de ordem. Seja, por exemplo, a sequência de pontos, traços e espaços, a seguir:

 

                                                                                              .                                 

A            B                C               D             E       F                ...............

 

            Esta sucessão de pontos, traços e espaços (pausas) corresponde ao sistema de códigos Morse ( homenagem à Samuel Morse, que patenteou o telégrafo em 1840 ).

 

Este exemplo nos mostra que :

           

            Sequência ou sucessão é qualquer conjunto onde seus elementos estão dispostos numa certa ordem.

 

Sequências Numéricas

 

            É todo o conjunto de números, que estão dispostos ordenadamente, de uma maneira que possamos indicar quais são os elementos desse conjunto.

 

Exemplo: A sequência de Fibonacci

                 Nesta sequência, cada elemento é formado pela soma dos dois elementos anteriores, ou seja: 1, 2, 3, 5, 8, 13, 21, .........

 

Representação de uma sequência

 

            Representamos a sequência numérica colocando os termos entre parênteses e separando-os por virgulas.

            Exemplo:

            (a₁, a₂, a₃, ......., a_n, .... ) onde  n  Î  N*

 

Estas sequências poderão ser:

            Finitas – quando o último termo é conhecido. Ex: (1, 4, 16).

            Infinitas – quando o último termo não é conhecido. Ex : (1, 8, 15, ...)

 

Leis de Formação

 

            Existem sequências numéricas em que os elementos ou termos estão dispostos de tal forma que não é possível relacioná-los com uma leis de formação.

            O exemplo famoso desta situação é a sequência dos números primos: (2, 3, 5, 7, ...)

            Para o estudo das sequências vamos supor sempre a possibilidade de relacionarmos as sequências por uma lei de formação. Podemos destacar dois tipos de leis de formação de uma sequência.

 

            1º caso – Fórmula do Termo Geral

            É uma fórmula que nos permite calcular um termo de ordem n em qualquer sequência.

            Exemplo: Dado a_n = 1 – 1/(n+1) para n Î N*

                             Calcular o produto dos 99 primeiros termos da sequência.

 

            Temos que:  a_n  =  n  /  (n+1), calculando os termos, a seguir:

 

            Quando n = 1, então a₁ = ½

                          n = 2 ,           a₂ = 2/3

                          n = 3 ,            a₃= ¾

            ......................................................

                          n = 98 .            a₉₈ = 98/99

                          n = 99 .             a₉₉ = 99/100

 

            Efetuando o produto dos termos da sequência, temos que:

 

            ½ . 2/3. ¾. 4/5.  ..... . 98/99. 99/100

           

            Como o denominador de um termo é igual ao numerador do termo seguinte, fazendo as simplificações, temos que:

 

            ½.2/3. ¾. 4/5.  ....... 98/99. 99/100  = 1/100

            Então, o produto dos 99 primeiros termos desta sequência é igual a 0,01.

 

            2º caso – Lei de recorrência

 

            Neste caso, é necessário recorrer a outros termos conhecidos (geralmente o primeiro) para se obter qualquer outro elemento da sequência, através de uma fórmula que forneça esta relação.

 

            Exemplo. Dado a_n+1= a_n (2^n-1 + 1)

                             Se a₃= 3, calcule a₅.

 

            Temos  a₃ = 3, logo

 

            n = 4 è a₃₊₁ = a₃ (2^3-1 + 1)

                            a₄ = a₃ (2²+ 1)

                            a₄ = a₃.5  è  a₄ = 15

 

            Como queremos a₅, temos então:

 

            a₄₊₁ = a₄ (2^4-1  + 1)

            a₅ = a₄(2³ + 1)

            a₅ = 15.9     è  a₅ = 135

 

Sequência como função

 

            Seja a sucessão de números ímpares (1, 3, 5, 7, 9, ....)

            Essa sequência de números ímpares é formada de acordo com uma regra ou lei de correspondência, na qual é possível estabelecer uma expressão f(n) que contenha a variável n e tal que para cada numeral natural {1, 2, 3, 4, 5, .....} atribuído a n se tenha a relação:

                                               a_n = f(n)

            Neste caso, dizemos que f(n) é o termo geral da sequência

 

            A lei de formação do conjunto de números ímpares é dada através do termos geral

 

                                               a_n = 2n –1  ou por f(n) = 2n –1

           

            Neste caso, podemos dizer que:

 

            Sequência é uma função cujo domínio é o conjunto dos naturais diferente de zero {1, 2, 3, ....} e cujas imagens formam o conjunto dos númeors reais, ou seja

                                               F : N* è R

 

Séries

 

            São expressões numéricas que resultam quando substituimos as vírgulas por sinais de adição entre os termos sucessivos de uma sequência.

            Exemplo:

            A sequência dos números triangulares 1, 3, 6, 10,..... pode ser decomposta assim:

 

            a₁ = 1

            a₂ = 1 + 2 = 3

            a₃ = 1 + 2 + 3 = 6

            a₄ = 1 + 2 + 3 + 4 = 10 ..........

 

            Assim, para encontrarmos o enésimo número triangular, devemos somar ostermos de uma sequência finita, de 1 até o número desejado, ou seja:

 

                                   a_n = 1 + 2 + 3 + 4 + 5 + 6 + ....... + n

            Exemplo. Determinar o décimo primeiro número triangular

                            a₁₁ = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 = 64

 

            Desta forma, podemos dizer que dada uma única sequência numérica (a₁, a₂, a₃, a₄, a₅, a₆, ... , a_n) formamos a sequência de somas (S₁, S₂, S₃, S₄, ....., S_n)

 

            Observamos que :

 

            S₁ = a₁

            S₂ = a₁ + a₂

            S₃ = a₁ + a₂ + a₃

            ............................

            S_n =a₁ + a₂ + a₃ ..... + a_n

 

            Fica, portanto, caracterizado o que chamamos de Série

 

            As séries também podem ser finitas (quando se conhece o último termo da série) ou infinitas (quando não se conhece o último termo).

            A representação de uma série é dada pelo símbolo E (somatório)

 

            Para a série finita temos a representação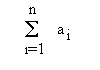

 

 

            E, para a série infinita é usada a representação

 

 

 

Exemplo prático de série

 

            Uma pessoa A, chega às 14 horas para um encontro com uma pessoa B. Como B não chegou, ainda, A resolveu esperar um tempo t1 = ½ hora, e após, t2 = ½ t1, e após, t3 = ½ t2, e assim sucessivamente. Se B não veio quanto temo A esperou até ir embora?

 

Pelos dados temos a seguinte sequência infinita:

 

            (30min, 15min, 7,5min, 3,75min, .........)

 

Para obter o valor da soma desta sequência, basta calcular o valor da série, ou seja:

 

            Sn = 30 + 15 + 7,5 + 3,75 + ........

Observamos que:

            S1 = 30min

            S2 = 30 + 15 = 45min

            S3 = 30 + 15 + 7,5 = 52,5min

            S4 = 30 + 15 + 7,5 + 3,75 = 56,25min

            ...................................

            S8 = 59,765625min

            .........................

 

            Podemos constatar que, conforme o número de termos vai aumentando, o valor de cada termo acrescentado vai diminuindo, aproximando-se cada vez mais de 60 minutos. Dizemos, neste caso, que a sequência converge para 60 minutos.

            Logo, a pessoa terá que esperar 60 minutos até ir embora.

Exercícios resolvidos e propostos

            1) A partir das sequências
a)1² = 1
2² = 1+2+1
3² = 1+2+3+2+1
..................
b) 1² = 1
11² = 121
111²
...................
Calcule o valor de A
A= (55555 x 55555) / 1+2+3+4+5+4+3+2+1 - 1000

Ora, pela sequência b, temos que:
1+2+3+4+5+4+3+2+1 = 5²
e, pela sequência a, temos que:
11111² = 123454321
Então, aplicando estes resultados na expressão A, temos que :
a= (5² x 123454321 ) / 5² - 10000
Logo, A=123453321

2) Uma sequência numérica é definida por:
a₁ = 1
a_n = a_n-1 + (-1)ⁿ para n >= 2
Determine a soma dos 6 primeiros termos.

Pelos dados temos que:
a₂ = 1 + (-1)² = 2
a₃ = 2 + (-1)³ = 1
a₄ = 1 + (-1)⁴ = 2
a₅= 2 + (-1)⁵ = 1
a₆ = 1 + (-1)⁶ = 2
Logo S₆ = 1+2+1+2+1+2 = 9

3) Qual é a soma da série: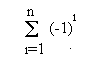


n= 1 ==> a₁ = -1
n = 2 ==>a₂ = 1
n = 3 ==> a₃ = -1
Então, se n é par a soma é zero e se n é impar a soma é igual a -1

Exercícios propostos:

1) Nasequência (a₁, a₂, a₃, ...., a_n, ....) cujo termo geral é a_n = n + 2(n+2), determine os 4 primeiros termos da sequência.
Resp: 7, 10, 13, 16

2) Sejam as sequências dos termos gerais
a_n = 2n+1
b_n=2n
c_na_n . b_n+1
Qual é o vigésimo termo da sequência de termo geraL c_n?
Resp: 1722

Expanda o somatório:

Resp: x + x²/3 + x³/5 + x⁴/7