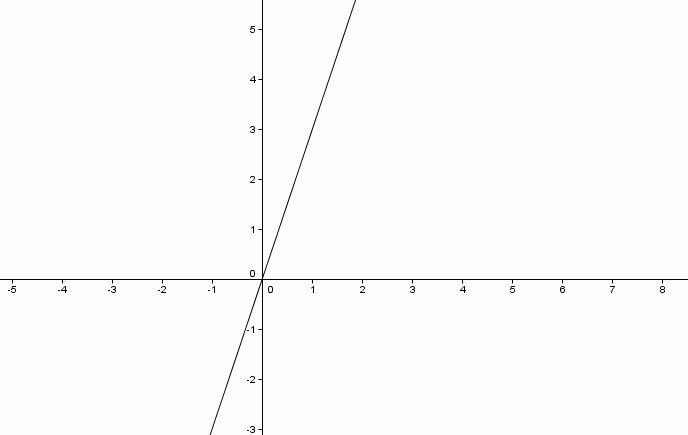
RESUMO DE AULA
UMA VISÃO DE FUNÇÃO COMO PROPORÇÃO
É muito comum, ao darmos os primeiros exercícios de função do primeiro grau, verificarmos que os alunos tendem a fazê-los usando proporções. Professor: Posso resolver por regra de três ? É a frase que escutamos.
Então, como queremos fixar os conceitos de função, particularmente as de primeiro grau, procuramos destacar o conceito dos coeficientes (angular e linear) da função y=ax + b para explicar os seus significados, afastando do aluno a interpretação da referida função como uma proporção, quando, na realidade, deveríamos fazê-lo associar esta interpretação como algo real, isto é, uma forma de interpretar o conceito de função.
Assim, deveríamos aproveitar a interpretação geométrica da função do primeiro grau, explicada ao aluno, para mostrar, visualmente, como ele pode visualizar a função como sendo uma proporção.
Para tal, na equação y = ax + b, fazendo b=0 (coeficiente linear) obtemos y = ax, caracterizando uma proporção, onde a (coeficiente angular) é o fator de proporção entre y e x, conforme gráfico abaixo:
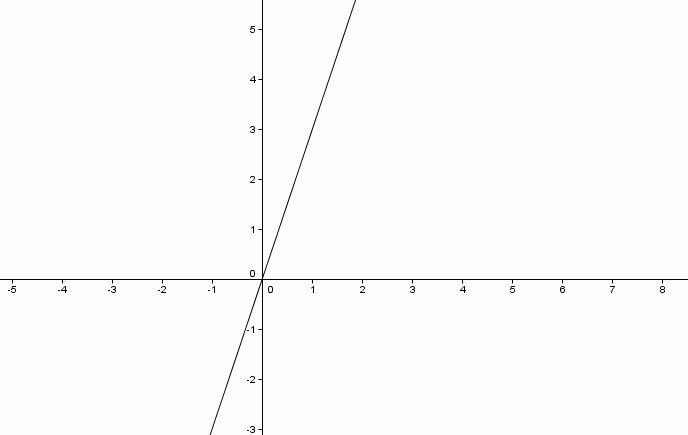
Da mesma forma, podemos caracterizar esta proporção direta, numa forma inversa y = a / x, conforme gráfico abaixo:
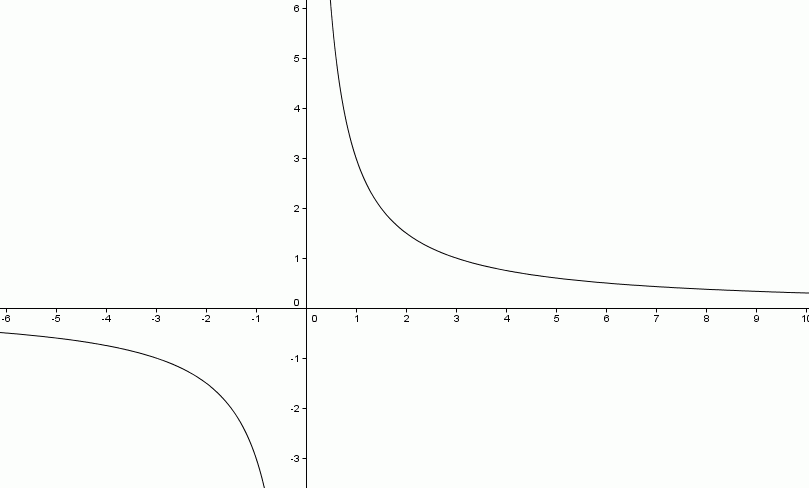
Sendo assim, podemos enunciar um problema de proporção em forma de função. Por exemplo, suponhamos que y seja diretamente proporcional a k, l, m e inversamente proporcional a p, r, s. Então, teríamos:
y = f(k, l, m, 1/p, 1/r, 1/s)
Para entendermos melhor, vamos ilustrar com alguns problemas de nosso dia-a-dia:
60 homens abriram um canal com 108 metros de comprimento, 1,5 m de largura e 3 metros de profundidade. Para isso, trabalharam 30 dias a 8h/dia. Com 54 homens, trabalhando 10h/dia, qual será o comprimento do canal com 2m de largura e 2,7m de profundidade, aberto em 40 dias (Rev. Cálculo-Matemática para todos)?
Solução:
Vamos descobrir a nossa constante de proporcionalidade da função (coeficiente angular). Sabemos que: 60 homens construiram um canal com 108m de comprimento, 1,5m de largura e 3m de profundidade em 30 dias, trabalhando 8h/dia.
O problema é descobrir um novo comprimento de canal, alterando-se as demais variáveis, ou seja, temos uma função em que o comprimento do canal depende dessas variáveis.
Vamos nomear essas variáveis:
h – homens trabalhando
c – comprimento do canal
g – largura do canal
p – profundidade do canal
t – horas trabalhadas por cada homem
d – dias trabalhando
Levando-se em conta o que afeta direta ou indiretamente o comprimento do canal, temos:
c = f(h, t, d, 1/g, 1/p)
Logo, usando a constante de proporcionalidade (coeficiente angular) da função, temos:
c = a . (h.t.d) / (g . p)
ou seja,
c = a . (60x30x8) / (1,5 x 3)
que nos dá o valor de a = 0,03375
Então, aplicando-se a na equação que desejamos calcular o novo comprimento, temos:
c = 0,03375 x (54x40x10) / (2 x 2,7)
que nos dá o valor de c = 135
Logo, o canal terá 135 metros de comprimento.
Para ir da cidade A a cidade B, gasto 15 horas com a velocidade de 80 km/h. Se aumentar 20 km/h na velocidade, em quanto tempo concluo a viagem ?
Temos que o tempo é função inversa da velocidade, ou seja,
t = f(1/v)
Logo, calculando a constante de proporcionalidade (coeficiente angular) da função, temos:
t = a . 1/v → 15 = a/80 → a = 1200
Usando os novos dados, temos:
t = 1200 . 1/100 → t = 12 horas.
Um pintor estima pintar uma escola em 36 dias. Se contratar 2 ajudantes, com igual capacidade de trabalho, em quantos dias farão a pintura da escola ?
Temos que o número de dias é o função inversa da quantidade de pintores, ou seja:
d = f (1/p)
Calculando-se o coeficiente angular da função, temos:
36 = a . 1/1 (1 pintor)
Logo, a = 36
Usando os novos dados, temos:
d = 36 . 1/3 ( 3 pintores)
Logo, d = 12 dias
Dez diagramadores, trabalhando 8 horas por dia, em 12 dias, paginaram 3/5 de um livro. Em seguida, dois diagramadores foram deslocados para outro serviço. Quantos dias serão necessários para os restantes terminarem a paginação do livro, se trabalharem 5h/dia ?
Temos que a quantidade de dias é inversamente proporcional ao número de diagramadores, inversamente proporcional ao número de horas trabalhadas por dia e diretamente proporcional ao número de páginas diagramadas.
Assim, podemos expressar a função como:
d = f (1/h, 1/t, p)
onde:
h – número de diagramadores
t – número de horas trabalhadas por dia
p – número de páginas diagramadas
Calculando o coeficiente angular da função, temos:
12 = a . 1/10 . 1/8 . 3/5
Logo, a = 1600
Usando os novos dados, para os 2/5 restantes da paginação, temos que:
d = 1600 . 1/8 . 1/5 . 2/5 → d = 400/25 → d= 16 dias
Na realidade, podemos verificar essa noção de proporcionalidade de uma forma geométrica. Seja a função y = ax apresentada anteriormente, representada no gráfico pela reta r.
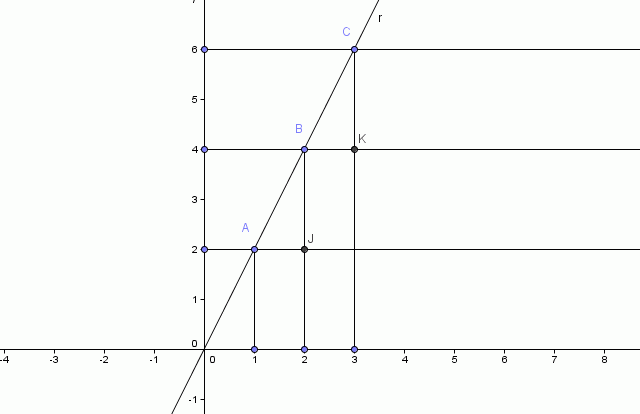
Verificamos que os triângulos BAJ e CBK são semelhantes logo,
BJ / AJ = CK / BK
Como ambas as razões determinam o coeficiente angular (a = tg α) da reta r, este se confunde com a razão de semelhança dos triângulos, ou seja, a razão (ou coeficiente) de proporcionalidade.
Verificamos que, mesmo que b (coeficiente linear) seja diferente de zero, este conceito de razão de proporcionalidade permanece, conforme gráfico abaixo:
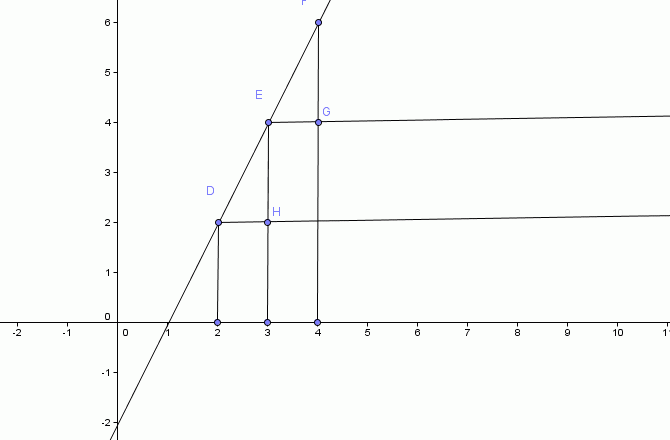
Isto significa que, mesmo que seja evidenciado o coeficiente linear (b), na equação y = ax + b, podemos resolver um problema de função do primeiro grau usando este conceito de proporcionalidade, desde que estejamos usando a mesma reta, ou seja, estejamos usando o mesmo coeficiente angular (a), que nada mais é o que acabamos de ver como razão de proporcionalidade ou também chamado por alguns de taxa média de cfrescimento ou decrescimento, dependendo se a função é crescente ou decrescente.