RESUMOS DE AULAS

Aula de 18/10/2011

Assunto : Inequações do 2° grau

Recordou-se o que foi ensinado no 2º Bimestre referente a equação do 2° grau, ou seja, a fórmula para se achar as raízes da equação e as coordenadas do vértice da parábola, muito importante para os cálculos de valores máximos e mínimos da função do 2° grau.

Destacou-se a importância, no estudo das inequações, quando as funções do 2° grau passam a ser positivas ou negativas (f(x)>0 ou f(x)<0). Graficamente, foi explicado, conforme abaixo:

a) Seja o gráfico da função x² – 5x + 6 = 0

Se calcularmos as raízes, temos:

x = (-b ± ÖD) / 2a onde D = b² – 4ac

Então:

x = (5±Ö1) / 2 onde podemos ter x₁ = 3 e x₂ = 2

Graficamente, teríamos:

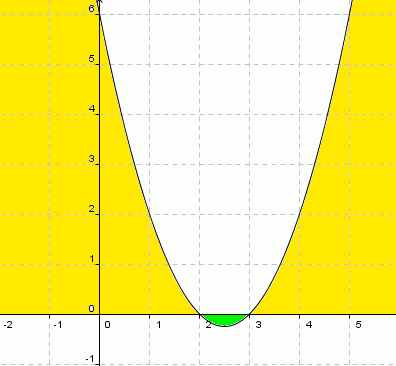
Em primeiro lugar, observemos que a parábola tem a concavidade para cima porque a > 0 ( o coeficiente do termo do 2° grau é positivo). Em seguida verificamos que os valores da função ficam negativos entre as raízes (2 e 3, conforme a cor verde) e, em todo o restante a função sempre será positiva (valores de x<2 ou valores de x>3, conforme a cor amarela)

b) Seja, agora, a função -x² + 5x - 6 = 0

Calculando as raízes, temos:

x = (-5±Ö1) / -2 onde x₁ = 2 e x₂ = 3

Graficamente, teríamos:

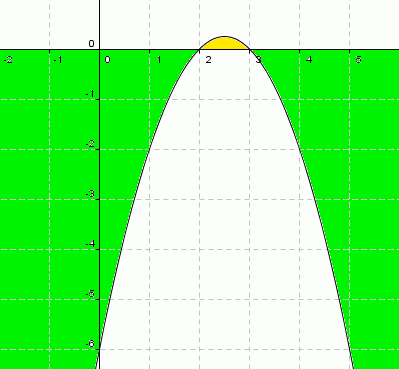
Em primeiro lugar, observemos que a parábola tem a concavidade para baixo porque a < 0 ( o coeficiente do termo do 2° grau é negativo). Em seguida verificamos que os valores da função ficam positivos entre as raízes (2 e 3, conforme a cor amarela) e, em todo o restante a função sempre será negativa (valores de x<2 ou valores de x>3, conforme a cor verde)

Concluímos, então, que para o estudo das inequações do 2° grau é necessário observar as raízes da equação (fornecendo os limites inferior e superior de x) e o coeficiente do termo do 2° grau (informando a concavidade da parábola).

Aula de 25/10/2011

Assunto : Continuação de inequações

O estudo das inequações do 2° grau se torna interessante quando temos de relacionar a função do 2° grau com outras funções, inclusive de 2° grau. Por exemplo, seja o sistema composto por:

x – 3 ³ 0

x² – 6x + 8 £ 0

Graficamente, temos:

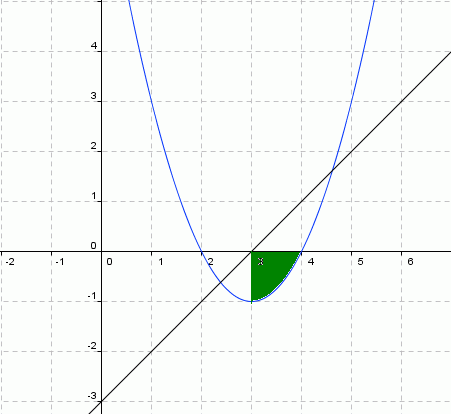
Verificamos que os valores de x que atendem ao sistema estão entre 3 e 4

( 3 £ x £ 4).

Por outro lado, o estudo das inequações do 2° grau pode nos auxiliar quando temos que analisar duas ou mais funções ligadas por uma operação de multiplicação ou de divisão. Por exemplo, seja o caso:

(x² – 4x + 3) . (x² -7x + 10) > 0

Graficamente, teríamos:

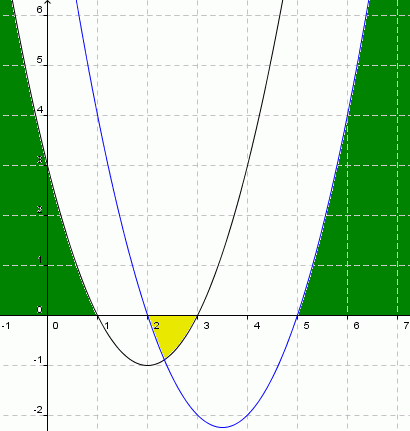
Notamos que a região de cor verde seria uma solução (x < 1 ou x> 5), assim como a região de cor amarela seria outra solução possível (2 < x < 3).

Podemos confirmar o gráfico com uma solução algébrica (sem auxílio gráfico), o que seria o esquema abaixo:

		1	2	3	5
a	x - 4x + 3	+	-	-	+	+
b	x - 7x +10	+	+	-	-	+
a . b		+	-	+	-	+

Notamos que (x² - 4x +3) (x²- 7x + 10) > 0 nos seguintes casos:

a) x² - 4x + 3 > 0 e x² -7x + 10 > 0

que nos dá a solução x < 1 ou x > 5 (região verde)

b) x² – 4x + 3 < 0 e x² – 7x + 10 < 0

que nos dá a solução 2 < x < 3 (região amarela)

Repare que a mesma solução seria válida se tivéssemos que resolver a inequação:

(x² – 4x + 3 ) / ( x² -7x + 10 ) > 0

Aula de 21/10/2011

Assunto: Estudo da função f(x) = sen x.

Vamos desenvolver um estudo das funções trigonométricas, começando pela função f(x) = sen x.

Seja o gráfico da função f(x) = sen x.

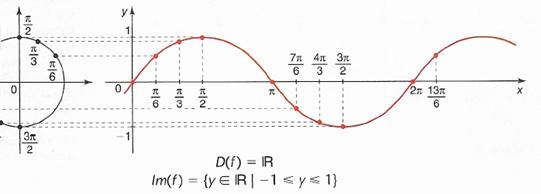
Verificamos, como sabemos, que f(x) = sen x é periódica, devido a repetição de seu traçado gráfico a cada 2π (circunferência completa). Assim, temos:

sen (x + 2π ) = sen x

sen (x + 4π ) = sen x

sen (x + 6π ) = sen x

sen (x + 8π ) = sen x ….....

e assim sucessivamente

Por este motivo, diz-se que o período da função f(x) = sen x é 2π

Além disso, verificamos no gráfico a possibilidade de modificarmos a altura dos picos (valores máximos e mínimos de f(x)) e a amplitude da curva (alongando ou estreitando). Tais possibilidades são utilizadas nos diversos tipos de osciloscópios existentes.

Assim, por exemplo, o gráfico da função f(x) = 3sen x seria:

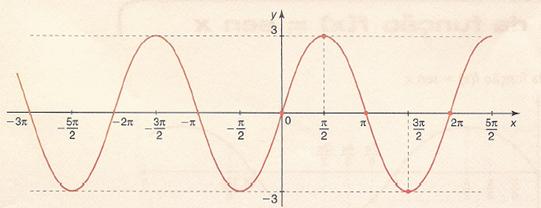
Repare que os limites passaram de -1 a +1 para -3 a + 3, destacando a altura dos picos.

Por outro lado, o gráfico da função f(x) = sen 2x, seria:

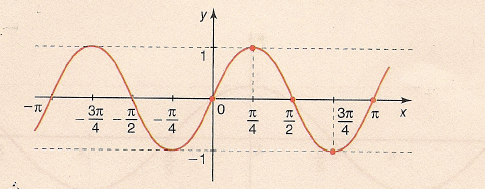
Repare que a amplitude da curva ficou mais estreita (na realidade, ficou reduzida a metade).

Sendo assim, podemos fazer várias operações com a função seno para verificarmos o seu comportamento.

Ilustrando, segue um exemplo prático do que foi estudado:

Aula de 25/10/2011

a) Trigonometria

Começamos a aula resolvendo o problema de trigonometria da última aula. Foi destacado que o movimento da roda gigante podia ser estudado por uma função trigonométrica, devido ao movimento da mesma ser cíclico, ou seja, o fenômeno se repete em ciclos bem determinados, no valor de 2π. Em termos trigonométricos, cada volta completa da roda gigante perfaz o período da função estudada, ou seja, 2π.

Assim, temos a função:

f(t) = 111 + 97sen πt/15

Lembramos que, se tivéssemos apenas f(t) = sen πt/15, os valores variariam de -1 a + 1, ou seja:

- 1 £ sen πt/15 £ +1

Como tínhamos 97sen πt/15, os valores passam a ser:

- 97 £ sen πt/15 £ +97

Isto porque ao multiplicarmos a função por 97, os valores extremos ficaram multiplicados por 97.

Como a função era f(t) = 111 + 97sen πt/15 teríamos que somar 111 a todos os membros das inequações.

Logo, teríamos:

111 - 97 £ 111 + sen πt/15 £ 111 + 97

ou seja,

14 £ 111 + sen πt/15 £ 208

Isto que dizer que o valor máximo da função seria 208, ou seja, a altura máxima da roda gigante seria de 208 metros

A seguir, recordou-se que, quando alteramos o ângulo da função, alteramos o período da mesma (estreitando ou alongando). Assim, foi explicada a fórmula, a seguir, para se calcular o período de uma função, ao alterarmos o ângulo da mesma.

Assim, temos, por exemplo:

f(x) = sen a.x, onde a é o multiplicador do ângulo x.

O cálculo do período é dado por:

p = 2π / | a |

Desta forma, voltando ao problema da roda gigante, temos : f(t) = 111 + 97sen πt/15 onde

a = π / 15.

Assim, calculando o período, temos p = 2π / |π / 15| = 30

Logo, a roda gigante dá uma volta completa em 30 minutos.

b) Álgebra

Na parte de álgebra, foi alertado aos alunos procederem operações com inequações de forma isolada e depois verificarem qual a solução que atende a operação que liga as referidas inequações, conforme aula anterior.

Assim, se tivermos:

(x² – 5x + 6) . (x² – 6x + 8) > 0,

devemos fazer as hipóteses possíveis, no caso:

a) x² – 5x + 6 > 0 e x² – 6x + 8 > 0 porque se ambas forem positivas, a multiplicação delas também será positiva

b) x² – 5x + 6 < 0 e x² – 6x + 8 < 0 porque se ambas forem negativas, a multiplicação delas também será positiva.

Depois, basta verificar se as soluções para cada hipótese são exclusivas ou podem ser simplificadas, conforme feito na aula anterior.

Finalmente, foi decidido preparar uma lista de exercícios para serem resolvidos pelos alunos e corrigidos, posteriormente, em sala. Desta forma, segue a lista:

1) Determine o conjunto solução de (-x² - x + 6) . (x² – 4x) > 0

2) Determine os valores de x para que (x² -8x + 12) . (x² – 5x) < 0

3) Dados f(x) = x² – 2x – 3 e g(x) = - x² + 4, determine os valores reais de x para que

f(x)/g(x) >0

4) Determinar os valores de m para que exista solução real na identidade: sen x = 2m – 3

5) Determine o período da função: f(x) = 2 sen(2x + π/3)

6) Um supermercado 24 horas conta seus clientes através da função

f(x) = 900 – 800sen π/12 x, onde f(x) é o número de clientes. Utilizando-se esta função, qual a diferença entre o número máximo de clientes e o número mínimo de clientes, dentro do supermercado, em um dia completo ?

Aula de 1/11/2011

Resolução dos exercícios da aula anterior.

1°) ( -x² –x +6 ) . (x² – 4x) > 0

1ª hipótese: -x² –x +6 > 0 e x² – 4x > 0

2ª hipótese: -x² –x +6 < 0 e x² – 4x < 0

Calculando as raízes:

-x² –x +6 = 0 è x = ( 1±Ö(1+24) ) / -2, logo x=(1±5) / -2 obtendo x₁= -3 e x₂ = 2

x² – 4x = 0 è x(x-4) = 0 , logo x₁= 0 e x₂ = 4

Se A = -x² –x +6 e B = x² – 4x, temos a situação abaixo:

	-3	0	2	4
A	-	+	+	-	-
B	+	+	+	-	+
A.B	-	+	+	+	-

Assim, na 1ª hipótese teríamos : - 3 < x < 2 e na 2ª hipótese 2 < x < 4, ou seja, o intervalo – 3< x < 4 atenderia a questão.

2ª ) (x² – 8x + 12) . (x² - 5x) < 0

1ª hipótese: x² – 8x + 12 < 0 e x² - 5x > 0

2ª hipótese: x² – 8x + 12 > 0 e x² - 5x < 0

Calculando as raízes:

x² – 8x + 12=0 è x = ( 8±Ö(64-48) ) /2 è x = (8±4) / 2 è x₁ = 6 e x₂ = 2

x² - 5x=0 è x(x-5)= 0 è x₁ = 0 e x₂ = 5

Se A = x² – 8x + 12 e B = x² - 5x, temos a situação abaixo:

	0	2	5	6
A	+	-	-	-	+
B	+	-	-	+	+
A.B	+	+	+	-	+

Observamos somente o intervalo 5<x<6 atendendo a questão

3ª ) Temos, então:

(x² – 2x – 3) / (-x² + 4) > 0

1ª hipótese: x² – 2x – 3 > 0 e -x² + 4 > 0

2ª hipótese: x² – 2x – 3 < 0 e -x² + 4 < 0

Calculando as raízes.

x² – 2x – 3 = 0 è x = ( 2±Ö(4+12) ) / 2 è x = (2±4) / 2 è x₁ = 3 e x₂ = -1

-x² + 4 = 0 è x² = 4 è x₁ = -2 e x₂ == 2

Se A = x² – 2x – 3 e B = -x² + 4, temos:

	-2	-1	2	3
A	+	+	-	-	+
B	-	+	+	+	+
A / B	-	+	-	-	+

Observando, temos que na 1ª hipótese -2<x<-1 ou x > 3, o que não temos na 2ª hipótese.

4ª ) como sabemos que -1 £ sen x £ 1, então temos:

-1 £ 2m – 3 £ 1 è 2 £ 2m £ 4 è 1 £ m £ 2

5ª ) Se f(x) = 2 sen (2x + π/3) è p = 2π / |2| = π rd.

6ª) Se f(x) = 900 – 800sen x π/12

Sabemos que: - 1 £ sen x π/12 £ 1

Multiplicando por -800, temos:

800 ³ -800 sen x π/12 ³ -800

Somando 900, temos 1700 ³ 900 -800 sen x π/12 ³ 100

Observamos que o número mínimo de cliente foi 100 e o número máximo foi de 1700. Logo a diferença é de 1600 clientes.

Aula de 4/11/2011

Hoje vamos analisar outras funções trigonométricas importantes.

Comecemos com a função f(x) = cos x

Observemos o gráfico desta função:

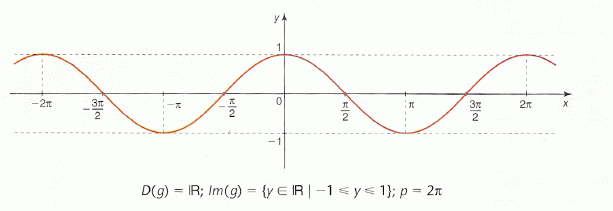
Verificamos ser muito semelhante à função f(x)= sen x, inclusive possui o mesmo período 2π.

Entretanto, o ponto de partida (ângulo de 0°) na função f(x) = sen x é de valor nulo, enquanto que na função f(x) = cos x, o ponto de partida é de valor unitário(já que cos 0° = 1). Devido a este comportamento semelhante entre f(x)= sen x e f(x)= cos x, o que foi detalhadamente estudado para a função f(x) = sen x vale também para a função f(x) = cos x.

Assim, temos, por exemplo, f(x) = 2cos x:

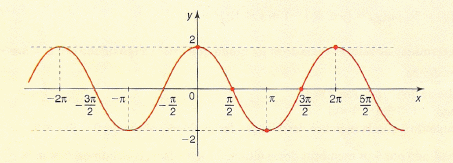
Verificamos a influência do coeficiente 2 aumentando os limites (picos), aumentando a amplitude da função.

Também, podemos ter, por exemplo, f(x) = 3cos 2x:

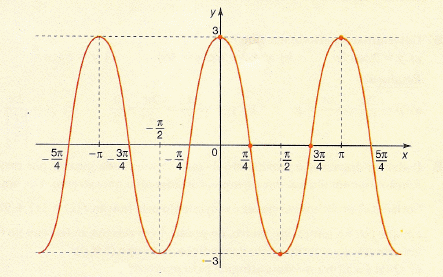
Verificamos a mesma influência na modificação do ângulo, estreitando o período (barriga) da função, além de aumentar a amplitude.

E, como o período é o mesmo, vale também a fórmula de cálculo do período de f(x) = cos a.x, ou seja:

p = 2π / |a|

Agora, vamos estudar a função tangente. Observemos o gráfico da função f(x) = tg x:

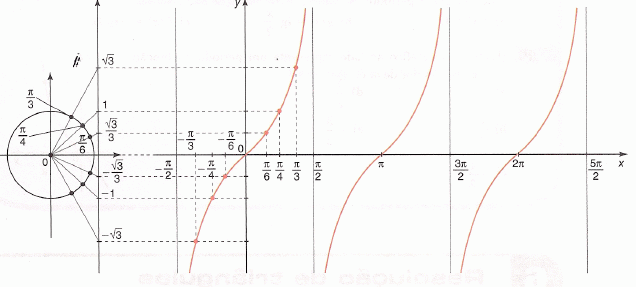
Verificamos que a curva apresenta pontos de descontinuidade nos ângulos:

..., -3π/2 , - π/2 , π/2, 3π/2, ......

Por esses pontos, traçando-se reta, verificamos que a curva tangencia sem tocá-las ( não há pontos de interseção). Essas retas são chamadas de assíntotas verticais.

Se lembrarmos que tg x = sen x / cos x, vemos que os pontos da forma x = π/2 + kπ com k pertencente ao conjunto dos inteiros não possuem tangente, pois, nesses casos, cos x = 0 e não existe divisão por zero.

Outra observação importante é que o ciclo se repete a cada π rd, e não a cada 2 π rd, como no caso do seno e do cosseno.

Agora, que já conhecemos as principais funções trigonométricas e algumas relações entre elas, tais como: sen² x + cos² x = 1 e tg x = sen x / cos x, assim como os valores dos principais ângulos (30°, 45° e 60°), nessas funções, podemos fazer muitos exercícios.

Antes disto, é interessante, para melhor entendimento dos problemas de funções trigonométricas, saber o significado dos termos das funções apresentadas. Assim, temos:

F(x) = a + btrig (cx + d), onde trig = sen, cos ou tg

a = significa o deslocamento no eixo das ordenadas para cima (a>0) ou para baixo(a<0)

b = significa aumento na amplitude(b inteiro) ou achatamento (b fracionário)

c = significa alargamento no período (c fracionário) ou estreitamento (c inteiro)

d = significa o deslocamento no eixo das abcissas para a direita (d<0) ou para a esquerda (d>0)

Se desejar entender melhor a influência dos parâmetros a, b, c e d, de uma forma lúdica, acesse os programas de números 12 em diante da seção Programas em geogebra. Lá você poderá movimentar esses parâmetros nas funções seno, cosseno e tangente e verificar dinamicamente o que acontece com as referidas funções:

Agora, finalmente, vamos a lista de exercícios:

1)Determine os valores de m para os quais é válida a função f(x) = cos x = (5m² – 2) / 2

2)Calcule o valor da expressão:

cos x + cos 2x + ... + cos 9x + cos 10x, para o valor x = π/3

3) Diga qual é o período e a imagem da função f(x) = ½ sen (x/4 + π)

4) Diga qual é a imagem e o período da função f(x) = -1 + 3cos (x + 4π/3)

5) O deslocamento horizontal de um pendulo é dado por f(t) = a. sen bt, em que f(t) é expresso em centímetros, t em segundos e a e b são constantes. Sabendo que certo pendulo f(t)= 7 sen 3πt, determine a amplitude e o período do movimento.

6)Para determinada maré, a altura h, medida em metros, acima do nível médio do mar, é definida por h(t) = 8 + 4sen(π/12 t), em que t é medido em horas. Determine o período de variação da altura da maré.

7) Determine os valores de m em f(x) = 2m + 5sen(2x/m + π/3), de modo que o período da função seja 5π

8)Determine o período de f(x) = - tg2x.

9)Considere as funções no campo real, definidas como f(x) = 2 – sen x/4 e g(x) = 2 + cos x/2. Calcule o valor de f(2π) . g(8π)

10)Uma máquina produz diariamente x dezenas de certo tipo de peça. Sabe-se que o custo da produção C(x) e o valor de venda V(x) são dados por: C(x) = 2 – cos x π/6 e V(x) = 3√2 sen x π/12, onde temos 0 ≤ x ≤ 6. Qual foi o lucro, em reais, obtido na produção de 3 dezenas de peças.

11)Seja a função f(x) = 2 – sen(πx – 3π/2). Determine o conjunto imagem dessa função.

12)Um atleta balança seus braços, segundo a função f(t) = π/9 sen[8π/3(t – ¾)], em que t é medido em segundos. Quantas oscilações completas (para frente e para trás) o atleta faz com o braço em 6 segundos ?

Resolvamos, um exercício, como exemplo:

Em uma animação, um mosquito aparece voando e sua trajetória no plano é dada pela função seguinte: y = 3.cos(bx +c). O período é de 6π e o movimento parte da origem, no sentido positivo do eixo das abcissas. Nestas condições mostre a função modelada para o voo do mosquito.

Foi dito que o movimento parte da origem, logo parte do ponto (0,0) da função dada. Assim, para x=0, temos y=0, logo:

0 = 3.cos(b.0 + c) = 3. cos ( c ) , então cos ( c ) = 0 , logo c = π/2

Sabemos que o período da função é dado por:

p = 2π / | b |

Como o período é conhecido, como 6π, temos que 6π = 2π / | b | , logo | b | = 2π / 6π

Temos, então, duas possibilidades: b = 1/3 ou b = -1/3. Como o valor – 1/3 não se aplica, ficamos com b = 1/3.

Assim, como b = 1/3 e c = π/2, temos a função y = 3.cos(1/3 x + π/2)

Os demais exercícios devem ser feitos pelos alunos, que devem tirar as suas dúvidas em sala de aula para a compreensão das soluções dos mesmos.

Aula 8/11/2011

Assunto: Aplicação das inequações do 2° grau

Esta aula e todas as demais as demais, serão apenas aulas práticas, onde serão resolvidos vários exercícios.

Nesta aula vamos dar um exemplo prático das inequações do 2° grau.

Seja uma empresa em que modelada a sua produção, chegou-se à função: y = x² + 2x + 2 e verificou-se uma outra função de restrição desta produção, da forma, y = -x + 2.

O objetivo efetivo da produção é que x² + 2x + 2 > 0 e -x + 2 < 0. Sendo assim, deseja-se saber, se x= milhares de unidades produzidas e y= receita, em reais obtida, qual será a região que essa restrição afetará a produção.

Vamos analisar as raízes de x² + 2x + 2 = 0

Temos; D = 4 – 8 = - 4 , logo D < 0 , portanto não tendo raízes reais, a curva da parábola está toda acima do eixo das abcissas, ou seja, qualquer valor de x, produzirá um y > 0

Analisemos –x + 2 = 0

Verificamos que todos os valores à direita de x=2, estão dentro da restrição.

Falta-nos, agora, verificarmos os pontos limites desta restrição na curva de produção. Então, se a curva de produção é y = x² + 2x + 2 > 0 e a restrição é y = -x + 2 < 0, basta verificarmos que os pontos acima de 2 ( x > 2) atendem às duas condições, conforme o gráfico abaixo:

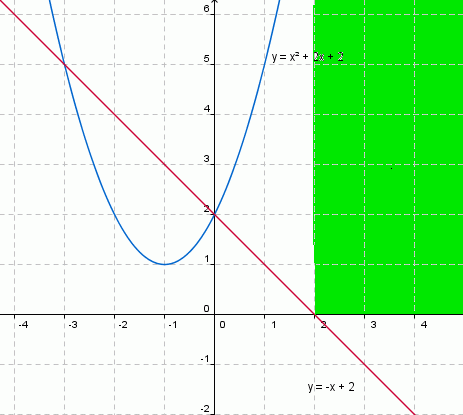
Logo, y(2)= 4+4+2=10, portanto com uma receita maior que R$10.000,00 a empresa já começaria a apresentar um resultado satisfatório, dentro de suas limitações.

Façamos outros exercícios semelhantes:

1) Que quantidade de peças atende a função x² – 2x -15 de produção de uma empresa, limitada pela função y = -x + 2, atendendo às seguintes condições: x² – 2x -15 > 0 e, também, que -x + 2 > 0 ?

2) A produção de uma empresa é representada pela função f(x) = x² – 8x + 12 e também pela função g(x)= x² – 5x. Se x, representa unidades produzidas, quantas unidades atenderiam a produção de f(x).g(x) > 0?

3) Se a receita de uma empresa é representada por f(x) = x / (x + 2) e a despesa é representada por g(x) = 1 / x, e x = unidades produzidas, a partir de quantas unidades produzidas a empresa apresentará lucro?

4) Se uma empresa tem como função de produção f(x)=x² – 7x + 12 e como função dependente da produção g(x) = x - 2 , como obter resultados positivos, se a dependência delas é exatamente f(x) / g(x). ?

5) Numa empresa foram modeladas três funções de produção, a saber:

f(x) = x – 4, g(x) = x² – 25 e h(x) = -x² +5x - 4

Se x representa o número de unidades produzidas, qual seria a produção necessária para que a modelagem de f(x) . g(x) / h(x) desse resultado positivo ?

Aula de 11/11/2011

Assunto : trigonometria

Nesta aula foram resolvidos alguns exercícios da lista dada anteriormente.

Assim, temos :

1) f(x) = cox x = (5m² – 2) / 2

logo,

-1 £ (5m² – 2) / 2 £ 1

-2 £ (5m² - 2 ) £ 2

então, temos : 5m² ³ 0 o que nos dá m ³ 0

5m² £ 4 o que nos dá m² £ 4/5

No primeiro caso, temos como condição m ³ 0

No segundo caso, temo que (m + 2√5/5)( m – 2√5/5) £ 0

o que nos conduz a duas hipóteses:

a) (m + 2√5/5) ³ 0 e (m - 2√5/5) £ 0

b) (m + 2√5/5) £ 0 e (m - 2√5/5) ³ 0

Resolvendo a primeira hipótese, juntamente com a condição, temos como solução que atenda a ambas : 0 £ m £ 2√5/5

A segunda hipótese não atende plenamente a condição, logo ficamos somente com a solução encontrada na primeira hipótese.

2)Temos que calcular cox + cos 2x + ......... + cos 9x + cos 10x , sabendo que x = π/3

Logo,

x = π/3=60° è cos 60° = ½

2x = 2. π/3 = 120° è cos 120° = -1/2

3x = 3. π/3 = 180° è cos 180° = -1

4x = 4. π/3 = 240° è cos 240° = -1/2

5x = 5. π/3 = 300° è cos 300° = ½

6x = 6. π/3 = 360° è cos 360° = 1

7x = 7. π/3 = 420° è cos 60° = ½

8x = 8. π/3 = 480° è cos 120° = -1/2

9x = 9. π/3 = 540° è cos 180° = -1

10x = 10. π/3 = 600° è cos 240° = -1/2

Somando as parcelas, temos – 1 - ½ = -3/2

Seja, agora, a resolução do último exercício da lista:

12) A função modelada para o movimento do braço é f(t) = π/9 sen [ 8π/3 ( t – ¾) ]

Precisamos achar o valor do período desta função ( o ciclo do braço para frente e para trás). Assim, temos:

p = 2π / (8π/3) = 2 . 3 / 8, ou seja, p = ¾ segundos

Então, o braço oscila uma vez ( 1 ciclo ) em ¾ de segundos. Por uma simples regra de três, em 6 segundos, o braço oscilará 8 vezes.

Aula de 18/11/2011

Assunto: Continuação de resolução de exercícios da aula de 4/11

3)Sabemos que:

-1 £ sen ( x/4 + π) £ +1

Então, para ½ sen ( x/4 + π) , teríamos:

-1/2 £ ½ sen ( x/4 + π) £ +1/2

Portanto, a imagem é [-1/2, +1/2]

Quanto ao período, temos : p = 2π / (1/4) = 8π

4) sabemos que:

-1 £ cos (x + 4π/3) £ +1

Então, para 3 cos (x + 4π/3) , teríamos:

-3 £ 3 cos (x + 4π/3) £ +3

Além disso, precisamos somar (-1) para chegarmos a função que queremos, logo :

-3 +(-1) £ (-1) + 3 cos (x + 4π/3) £ +3 + (-1)

o que nos dá:

-4 £ -1 + 3 cos (x + 4π/3) £ + 2

Logo, a imagem é [-4, 2]

O período será : p = 2π / 1 = 2π

6) Foi dado que h(t) = 8 + 4sen (π/12 t)

O período de variação será, portanto: p = 2π / (π/12) = 24 horas

9)Temos que:

f(x) = 2 – sen x/4 e g(x) = 2 + cos x/2

Queremos o valor de f(2π) . g(8π)

Assim,

f(2π) = 2 – sen 2π/4 = 2 – sen π/2 = 2 – 1 = 1

f(8π) = 2 + cos 8π/2 = 2 + cos 4π = 2 + 1 = 3

Logo,

f(2π) . g(8π) = 1 . 3 = 3

Aula 22/11/2011

Assunto: Continuação da resolução dos exercícios da aula de 8/11/2011

Nesta aula é dada continuidade aos exercícios com conteúdo de uma empresa, em suas funções de produção e limitação de produção.

Assim, temos:

1) Temos f(x) = x² – 2x – 15 > 0 limitada por g(x) = -x + 2 > 0

Calculando as raízes, temos para x² – 2x – 15 =0,

x = (2±8)/ 2 o que nos dá x₁ = 5 e x₂ = -3

Em relação a -x + 2 = 0 , temos x = 2

Fazendo o esquema, temos:

	-3	2	5
x^2 – 2x – 15	+	-	-	+
-x + 2	+	+	-	-

Verificamos que, a única situação que atende f(x) > 0 e g(x) > 0 seria x < -3, o que não se aplica a referida empresa, pois teria que produzir um número negativo de peças, o que é impossível.

2) Temos que as funções de produção são f(x) = x² -8x + 12 e g(x)= x² – 5x e queremos que f(x) . g(x) > 0

Calculemos as raízes de cada função.

Para x² -8x + 12 = 0 è x = (8±4) /2 , ou seja, x₁ = 6 e x₂ = 2

Para x² – 5x = 0 è x(x – 5) = 0 è , ou seja, x₁ = 0 e x₂ = 5

Fazendo o esquema, temos:

	0	2	5	6
a) x^2 -8x + 12	+	+	-	-	+
b) x^2 – 5x	+	-	-	+	+
a . b	+	-	+	-	+

Notamos que para a produção da empresa não serve a produção negativa, portanto, sórestaria as possibilidades: 2 < x < 5 e x > 6, porém a melhor delas ( produção positiva) seria x > 6, ou seja , a produção deveria ser maior de 6 peças.

3) Temos que :

f(x) = x / (x + 2) (receita)

g(x) = 1/x (despesa)

A função lucro seria : f(x) – g(x), que deveria ser f(x) – g(x) > 0.

Então:

x / (x + 2) - 1/x > 0

ou seja,

(x² – x – 2) / (x² + 2x) > 0

Calculando as raízes, temos:

Para x² – x – 2 = 0 è x = (1±3) / 2 , ou seja, x₁ = 2 e x₂ = -1

Para x² + 2x = 0 è x(x + 2) = 0, ou seja, x₁ = 0 e x₂ = -2

Fazendo o esquema, temos:

	-2	-1	0	2
a) x^2 – x – 2	+	+	-	-	+
b) x^2 + 2x	+	-	-	+	+
a/b	+	-	+	-	+

Como a produção não pode ser negativa, o que atenderia às funções seria x > 2, ou seja a produção não poderia ser menor que 2 peças.