RESUMOS DE AULAS

Aula de 18/10/2011

Assunto : Inequações do 2° grau

Recordou-se o que foi ensinado no 2º Bimestre referente a equação do 2° grau, ou seja, a fórmula para se achar as raízes da equação e as coordenadas do vértice da parábola, muito importante para os cálculos de valores máximos e mínimos da função do 2° grau.

Destacou-se a importância, no estudo das inequações, quando as funções do 2° grau passam a ser positivas ou negativas (f(x)>0 ou f(x)<0). Graficamente, foi explicado, conforme abaixo:

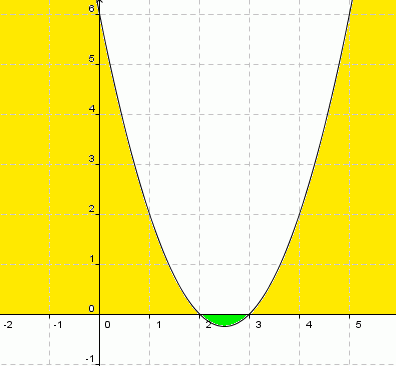
1. Seja o gráfico da função x² – 5x + 6 = 0

Se calcularmos as raízes, temos:

x = (-b  ) / 2a onde  = b² – 4ac

Então:

x = (51) / 2 onde podemos ter x₁ = 3 e x₂ = 2

Graficamente, teríamos:

Em primeiro lugar, observemos que a parábola tem a concavidade para cima porque a > 0 ( o coeficiente do termo do 2° grau é positivo). Em seguida verificamos que os valores da função ficam negativos entre as raízes (2 e 3, conforme a cor verde) e, em todo o restante a função sempre será positiva (valores de x<2 ou valores de x>3, conforme a cor amarela)

2. Seja, agora, a função -x² + 5x - 6 = 0

Calculando as raízes, temos:

x = (-51) / -2 onde x₁ = 2 e x₂ = 3

Graficamente, teríamos:

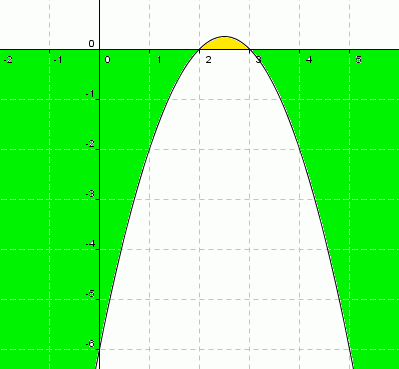
Em primeiro lugar, observemos que a parábola tem a concavidade para baixo porque a < 0 ( o coeficiente do termo do 2° grau é negativo). Em seguida verificamos que os valores da função ficam positivos entre as raízes (2 e 3, conforme a cor amarela) e, em todo o restante a função sempre será negativa (valores de x<2 ou valores de x>3, conforme a cor verde)

Concluímos, então, que para o estudo das inequações do 2° grau é necessário observar as raízes da equação (fornecendo os limites inferior e superior de x) e o coeficiente do termo do 2° grau (informando a concavidade da parábola).

Aula de 25/10/2011

Assunto : Continuação de inequações

O estudo das inequações do 2° grau se torna interessante quando temos de relacionar a função do 2° grau com outras funções, inclusive de 2° grau. Por exemplo, seja o sistema composto por:

x – 3  0

x² – 6x + 8  0

Graficamente, temos:

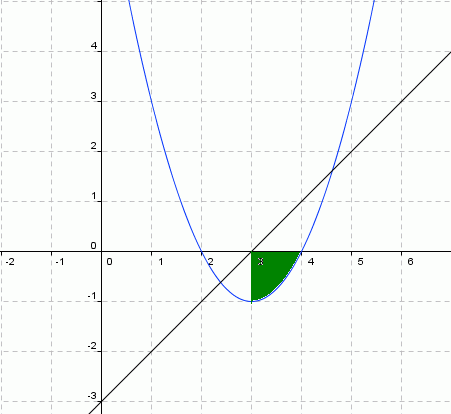
Verificamos que os valores de x que atendem ao sistema estão entre 3 e 4

( 3  x  4).

Por outro lado, o estudo das inequações do 2° grau pode nos auxiliar quando temos que analisar duas ou mais funções ligadas por uma operação de multiplicação ou de divisão. Por exemplo, seja o caso:

(x² – 4x + 3) . (x² -7x + 10) > 0

Graficamente, teríamos:

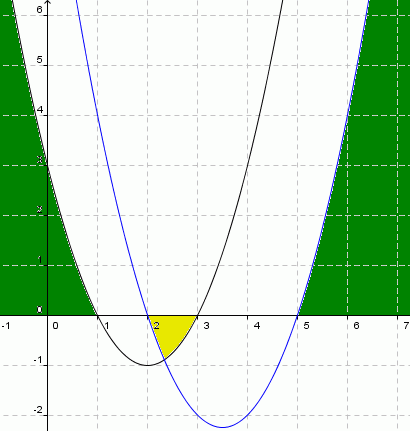
Notamos que a região de cor verde seria uma solução (x < 1 ou x> 5), assim como a região de cor amarela seria outra solução possível (2 < x < 3).

Podemos confirmar o gráfico com uma solução algébrica (sem auxílio gráfico), o que seria o esquema abaixo:

Notamos que (x² - 4x +3) (x²- 7x + 10) > 0 nos seguintes casos:

a) x² - 4x + 3 > 0 e x² -7x + 10 > 0

que nos dá a solução x < 1 ou x > 5 (região verde)

b) x² – 4x + 3 < 0 e x² – 7x + 10 < 0

que nos dá a solução 2 < x < 3 (região amarela)

Repare que a mesma solução seria válida se tivéssemos que resolver a inequação:

(x² – 4x + 3 ) / ( x² -7x + 10 ) > 0

Aula de 21/10/2011

Assunto: Estudo da função f(x) = sen x.

Vamos desenvolver um estudo das funções trigonométricas, começando pela função f(x) = sen x.

Seja o gráfico da função f(x) = sen x.

Verificamos, como sabemos, que f(x) = sen x é periódica, devido a repetição de seu traçado gráfico a cada 2π (circunferência completa). Assim, temos:

sen (x + 2π ) = sen x

sen (x + 4π ) = sen x

sen (x + 6π ) = sen x

sen (x + 8π ) = sen x ….....

e assim sucessivamente

Por este motivo, diz-se que o período da função f(x) = sen x é 2π

Além disso, verificamos no gráfico a possibilidade de modificarmos a altura dos picos (valores máximos e mínimos de f(x)) e a amplitude da curva (alongando ou estreitando). Tais possibilidades são utilizadas nos diversos tipos de osciloscópios existentes.

Assim, por exemplo, o gráfico da função f(x) = 3 sen x seria:

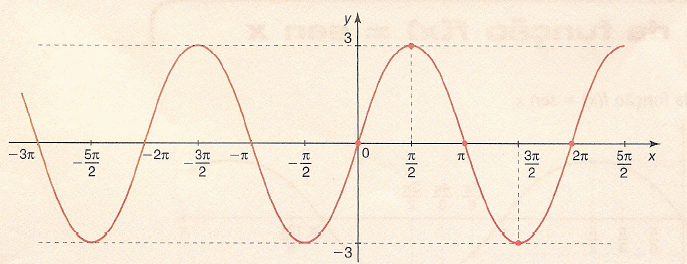
Repare que os limites passaram de -1 a +1 para -3 a + 3, destacando a altura dos picos.

Por outro lado, o gráfico da função f(x) = sen 2x, seria:

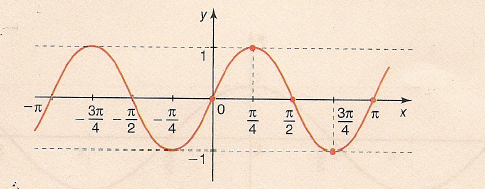
Repare que a amplitude da curva ficou mais estreita (na realidade, ficou reduzida a metade).

Sendo assim, podemos fazer várias operações com a função seno para verificarmos o seu comportamento.

Ilustrando, segue um exemplo prático do que foi estudado:

Aula de 25/10/2011

a) Trigonometria

Começamos a aula resolvendo o problema de trigonometria da última aula. Foi destacado que o movimento da roda gigante podia ser estudado por uma função trigonométrica, devido ao movimento da mesma ser cíclico, ou seja, o fenômeno se repete em ciclos bem determinados, no valor de 2π. Em termos trigonométricos, cada volta completa da roda gigante perfaz o período da função estudada, ou seja, 2π.

Assim, temos a função:

f(t) = 111 + 97sen πt/15

Lembramos que, se tivéssemos apenas f(t) = sen πt/15, os valores variariam de -1 a + 1, ou seja:

- 1  sen πt/15  +1

Como tínhamos 97sen πt/15, os valores passam a ser:

- 97  sen πt/15  +97

Isto porque ao multiplicarmos a função por 97, os valores extremos ficaram multiplicados por 97.

Como a função era f(t) = 111 + 97sen πt/15 teríamos que somar 111 a todos os membros das inequações.

Logo, teríamos:

111 - 97  111 + sen πt/15  111 + 97

ou seja,

14  111 + sen πt/15  208

Isto que dizer que o valor máximo da função seria 208, ou seja, a altura máxima da roda gigante seria de 208 metros

A seguir, recordou-se que, quando alteramos o ângulo da função, alteramos o período da mesma (estreitando ou alongando). Assim, foi explicada a fórmula, a seguir, para se calcular o período de uma função, ao alterarmos o ângulo da mesma.

Assim, temos, por exemplo:

f(x) = sen a.x, onde a é o multiplicador do ângulo x.

O cálculo do período é dado por:

p = 2π / | a |

Desta forma, voltando ao problema da roda gigante, temos : f(t) = 111 + 97sen πt/15 onde

a = π / 15.

Assim, calculando o período, temos p = 2π / |π / 15| = 30

Logo, a roda gigante dá uma volta completa em 30 minutos.

b) Álgebra

Na parte de álgebra, foi alertado aos alunos procederem operações com inequações de forma isolada e depois verificarem qual a solução que atende a operação que liga as referidas inequações, conforme aula anterior.

Assim, se tivermos:

(x² – 5x + 6) . (x² – 6x + 8) > 0,

devemos fazer as hipóteses possíveis, no caso:

a) x² – 5x + 6 > 0 e x² – 6x + 8 > 0 porque se ambas forem positivas, a multiplicação delas também será positiva

b) x² – 5x + 6 < 0 e x² – 6x + 8 < 0 porque se ambas forem negativas, a multiplicação delas também será positiva.

Depois, basta verificar se as soluções para cada hipótese são exclusivas ou podem ser simplificadas, conforme feito na aula anterior.

Finalmente, foi decidido preparar uma lista de exercícios para serem resolvidos pelos alunos e corrigidos, posteriormente, em sala. Desta forma, segue a lista:

1. Determine o conjunto solução de (-x² - x + 6) . (x² – 4x) > 0

2. Determine os valores de x para que (x² -8x + 12) . (x² – 5x) < 0

3. Dados f(x) = x² – 2x – 3 e g(x) = - x² + 4, determine os valores reais de x para que

f(x)/g(x) >0

4. Determinar os valores de m para que exista solução real na identidade: sen x = 2m – 3

5. Determine o período da função: f(x) = 2 sen(2x + π/3)

6. Um supermercado 24 horas conta seus clientes através da função

f(x) = 900 – 800sen π/12 x, onde f(x) é o número de clientes. Utilizando-se esta função, qual a diferença entre o número máximo de clientes e o número mínimo de clientes, dentro do supermercado, em um dia completo ?