Uma Revisão de Assuntos Importantes Ensinados no Ensino Fundamental

Vamos fazer uma pequena revisão de alguns temas importantes aprendidos no Ensino Fundamental. Esta revisão mostrará como você está para poder absorver bem os novos temas que aprenderá no Ensino Médio.

1) FATORAÇÃO

Vamos dividir este tema em duas partes: a fatoração numérica e a fatoração algébrica:

a) Fatoração Numérica

Qualquer número inteiro positivo pode ser decomposto em uma multiplicação de números primos (aqueles que são divididos apenas por eles mesmos ou a unidade).

Ex:

6 = 2 x 3

15 = 3 x 5

20 = 2 x 2 x 5 = 2² x 5

...........

Quando um número for grande (centenas, milhares, ...), vai-se dividindo, pouco a pouco, pelos números primos.

Ex:

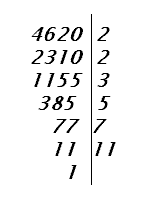
ou seja, 4620 = 2² x 3 x 5 x 7 x 11

b) Fatoração Algébrica

Para fatorar polinômios, de maneira geral, precisamos saber colocar em evidência os termos comuns e conhecermos alguns produtos notáveis. A título de recordação, eis alguns produtos notáveis:

A² - B² = (A + B) . (A – B)

(A + B)² = A² + 2AB + B²

(A – B)² = A² – 2AB + B²

(A + B)³ = A³ + 3A ²B + 3AB² + B³

(A - B)³ = A³ - 3A ²B + 3AB² - B³

Assim, seja a decomposição de x²y + 4xy + 4y

Como y é comum, colocando-o em evidência, temos:

y(x² + 4x + 4)

Verificando o produto notável entre parênteses temos:

y(x+2)²

Logo, x²y + 4xy + 4y = y(x+2)²

2) MÁXIMO DIVISOR COMUM E MÍNIMO MÚLTIPLO COMUM

Sabendo-se fatorar, podemos descobrir o mdc (máximo divisor comum) e o mmc (mínimo múltiplo comum) entre dois ou mais números ou entre duas ou mais expressões algébricas.

Como regra, devemos lembrar que:

a) mdc

Devemos procurar apenas os fatores (termos) comuns elevados aos menores expoentes.

b) mmc

Devemos procurar todos os fatores (termos) comuns e não comuns elevados aos maiores expoentes.

Ex; 750 e 540

Fatorando-os, temos:

750 = 2 x 3 x 5³

540 = 2² x 3³ x 5

Então, temos:

mdc = 2 x 3 x 5 = 30

mmc = 2² x 3³ x 5³ = 27000

Se fossem expressões algébricas, seria a mesma coisa, considerando-se os termos comuns e não comuns.

Ex: x³ + 2x² + x e x³ -2x² + x

Fatorando-se, temos:

x³ + 2x² + x = x(x² + 2x + 1) = x(x+1)²

x³ - 2x² + x = x(x² - 2x + 1) = x(x-1)²

Então, temos:

mdc = x

mmc = x . (x+1)². (x-1)²

3) NÚMEROS FRACIONÁRIOS

Todo número que se expresse por a/b, onde b¹0 é chamado de número fracionário, onde a(numerador) representa a parte tomada da unidade e b(denominador) representa em quantas partes foi dividida a unidade.

Ex: 3/8

Significa que dividiu-se a unidade em 8 partes e foram tomadas 3 dessas partes.

Para se somar ou subtrair números fracionários é necessário que as partes estejam divididas da mesma forma.

Ex ; 3/8 + 1/8 = 4/8

Se as unidades não estiverem divididas da mesma forma (denominadores diferentes), devemos achar frações correspondentes para poder efetuar a operação.

Ex: 3/8 + 1 / 4

Neste caso, os denominadores 8 e 4 mostram que a unidade foi dividida diferentemente. Então devemos achar a fração correspondente de ¼, cujo denominador seja 8. Seria algo assim:

1/ 4 = ? / 8

Verificamos que 8 = 4 x 2. Logo a fração correspondente teria o seu numerador multiplicado por 2, ou seja 1 / 4 = 2/8

Agora, podemos voltar e fazer a soma 3/8 + 1 / 4, ou melhor 3/8 + 2/8 = 5/8

Na realidade, o que fazemos é procurar o mmc entre os denominadores para poder somar ou subtrair as frações. Por exemplo:

Somar 1 / 2 + 3 / 4 + 1 / 8

Como o mmc é 8 ( entre 2, 4 e 8), então seria o mesmo que somar:

4 / 8 + 6 / 8 + 1 / 8 = 11 / 8 ou 1 3/8

Para multiplicarmos as frações, basta multiplicarmos os numeradores e os denominadores, respectivamente.

Ex ; 3 / 4 . 1 / 5 = 3 / 20

Para dividirmos frações basta multiplicarmos a primeira pelo inverso da segunda.

Ex: 3 / 4 : 2 / 5 = 3 / 4 . 5 / 2 = 15 / 8

4) NÚMEROS DECIMAIS

Todo a fração cujo denominador seja uma potência de 10 pode ser transformado num número chamado de decimal.

Ex:

3 / 10 = 0,3

5 / 100 = 0,05

.......

Na realidade, o número decimal é o resultado da divisão entre o numerador e o denominador. A utilização da expressão decimal é importante devido ao uso corrente de porcentagem. É comum em nosso dia-a-dia comprarmos ou vendermos objetos com algum desconto ou lucro. Isto acaba exigindo uma certa necessidade em trabalhar com números decimais.

Exemplo:

Uma calça custa R$78,00. Porém o vendedor dá um desconto de 30%. Qual é o valor desse desconto?

Assim, se nos lembrarmos que 30% é o mesmo que 30 / 100 = 0,30, basta multiplicarmos 78,00 x 0,30 = 23,40.

Logo, o desconto dado na calça é de R$23,40.

5) POTENCIAÇÃO

A repetição de um mesmo fator na decomposição de um número pode ser expressa na forma de uma potência.

Ex:

27 = 3 x 3 x 3 = 3³

32 = 2 x 2 x 2 x 2 x 2 = 2⁵

Na forma geral, temos a^b , onde a é conhecido como base e b como expoente. Assim, para operarmos potências da mesma base basta somar os expoentes na multiplicação ou subtrairmos os expoentes na divisão

Ex:

2⁵ . 2² = 2⁷

2⁵ : 2² = 2³

Uma potência negativa significa a inversão da base elevada a esta potência.

Ex:

2^-5= (1/2)⁵ = 1 / 32

(2/3)^-2 = (3/2)² = 9/4

Se a potência for uma fração, estaremos, na realidade, expressando uma radiciação, na forma:

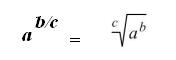
Ex:

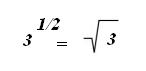
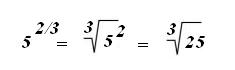
Assim, para procedermos com as operações entre raízes, podemos transformá-las em potências de expoentes fracionários:

Ex:

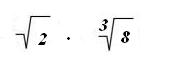
Teremos:

2^1/2 . (2³)^1/3 =

2^1/2 . 2^3/3 =

2^1/2 . 2 =

2^{1/2 + 1} = 2^3/2

ou seja

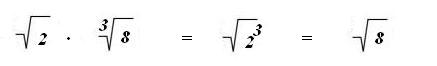
6) RAZÃO E PROPORÇÃO

Um número fracionário expresso na forma a/b (b¹0) também pode ser conhecido como razão. Assim, ¾, também pode ser interpretado como a razão de 3 para 4, ou seja, das quatro partes da unidade tomam-se 3 partes. Quando duas razões representam o mesmo valor dá-se o nome de proporção.

Assim, ¾ = 6/8, ou seja, tomar 3 de 4 partes da unidade é o mesmo que tomar 6 partes de 8 partes da unidade. É importante conhecer a nomenclatura das proporções.

Se a/b = c/d, temos:

a,d è chamados de extremos da proporção

b,c è chamados de meios da proporção

Uma propriedade importante das proporções é que o produto dos meios é igual ao produto dos extremos, ou seja:

Se a/b = c/d , então ad = bc

Ex: ¾ = 6/8 pois 3.8 = 6.4

Outra propriedade importante, mas pouco usada, é que a soma dos numeradores e denominadores das razões continua em proporção com cada razão. Assim,

Se 3/ 4 = 6 / 8 Logo, (3+6) / (4 + 8) = 3 / 4 = 6 /8

Ou seja,

9 / 12 = 3 / 4 = 6 / 8